How to Know Which Parameter Makes Best Predictor Linear Model

When choosing a linear model these are factors to keep in mind. LinearRegression lr new LinearRegression.

How To Interpret P Values And Coefficients In Regression Analysis Statistics By Jim

The form is linear in the parameters because all terms are either the constant or a parameter multiplied by an independent variable IV.

. Eric Skiff - Chibi Ninjahttpfreemu. Up to 5 cash back Linear Predictor. However now I want to manually change number 30 in front of memory variable to say 60 so it becomes.

Find the best linear predictor from a time series model and the mean squared prediction errorThanks for watching. The predicted value for the response variable. Trying to model it with only a sample doesnt make it any easier.

Where x s are the variables and β s are the parameters. Make sure this model has equally distributed residuals around zero. The value for the predictor variable.

The first line of code makes the linear model and the second line prints out the summary of the model. If you change the equation to. Pretend the left-censored predictor is not censored but has a discontinuity in its relationship with Y at the censoring point and have a second Y variance parameter for those observations to reflect incomplete conditioning on X X c instead of X x.

We will also find the variance of the error made by this best predictor. Find a model with a high adjusted R2. In matrix form the model is expressed as where Y and 3 are.

You can also compare coefficients to select the best predictor Make sure you have normalized the data before you perform regression and you take absolute value of coefficients You can also look change in R-squared value. Y β 0 β 1 x 1 β 2 x 2 ϵ. In conclusion in this post we showed how to do prediction with k-fold cross validation using linear mixed models.

Here y is a linear function of β s linear in parameters and also a linear function of x s linear in variables. Incomehappinesslm. Regularizing a Linear Predictor.

ŷ β0 β1x where. The structure of the model relates each observed y value to a predicted value. Begingroup I wonder how well this approach would work.

Y cd cT Xd Y c d c T X d. Generally variable with highest correlation is a good predictor. Make sure the errors of this model are within a small bandwidth.

Where µ is the grand mean α. Everything is the same as one-way just a few parameters get added in the equation. Its a method provided by the sklearn library which allows us to define a set of possible values we wish to try for the given model and it trains on the data and identifies the best estimator from a combination of parameter values.

Only compare linear models for the same dataset. In a simple way the equation can be written as. In this post well review some common statistical methods for selecting models complications you may face and provide some practical advice for choosing the best regression model.

The average change in the response variable for a one unit increase in x. Price 300 60 memory 56 screen_size 12. So I would favor the right model.

Choosing the correct linear regression model can be difficult. A linear regression equation simply sums the terms. To evaluate the simple linear regression model we compare the model to a baseline model with only a response variable.

A simple linear regression model takes the following form. Consider an equation of the form. Dataset vectorData assemblertransform dataset.

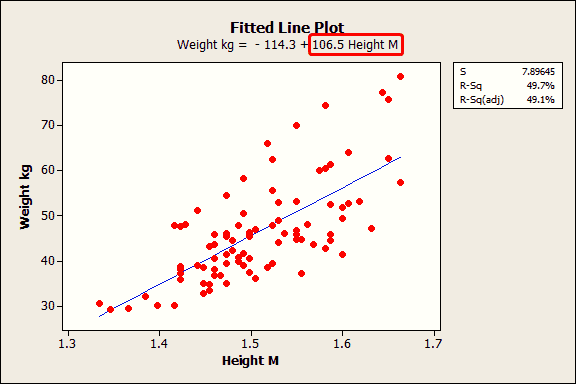
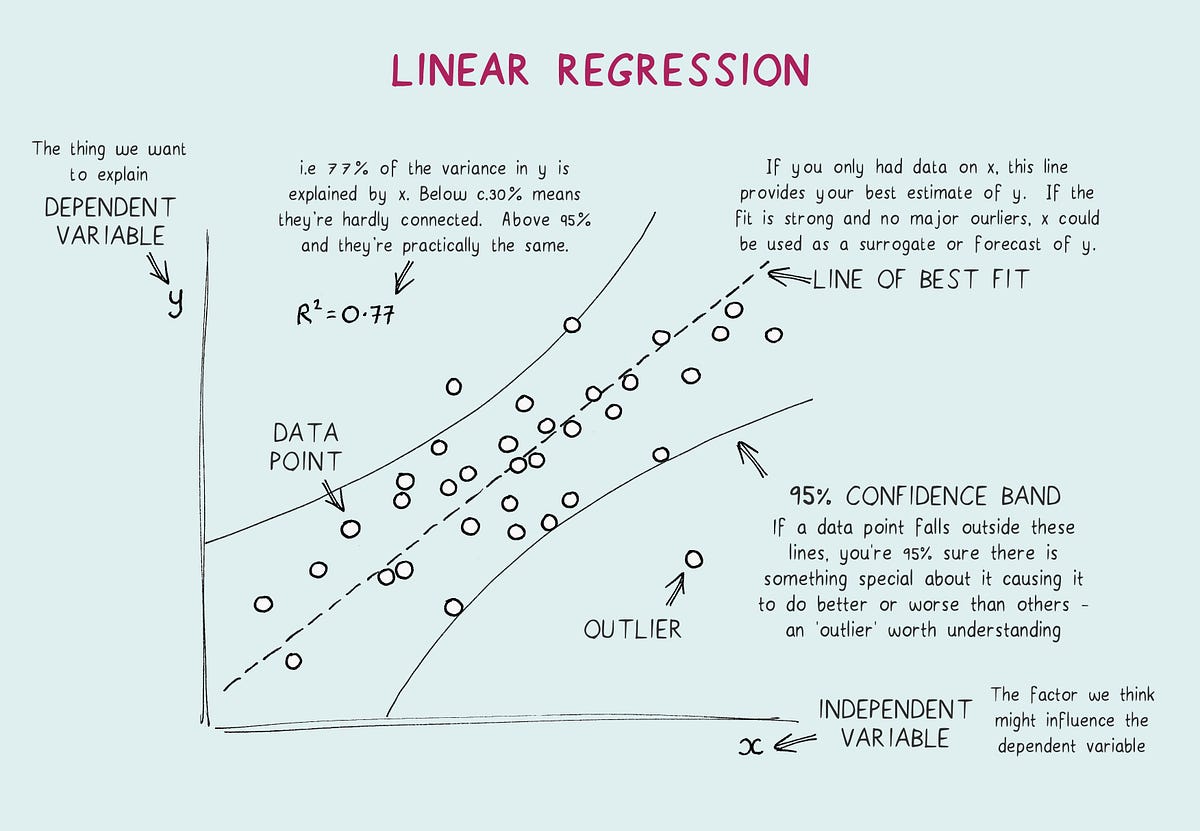
Y β 0 β 1 x 1 β 2 x 1 2 ϵ. The predicted value is obtained by transformation of the value emerging from the linear predictorThe linear predictor η eta is a linear sum of the effects of one or more explanatory variables x j. The R² value also known as coefficient of determination tells us how much the predicted data denoted by y_hat explains the actual data denoted by y.

R-Squared R² y dependent variable values y_hat predicted values from model y_bar the mean of y. Where the xs are the values of the p different explanatory. Linear regression is one of the most commonly used predictive modelling techniquesIt is represented by an equation 𝑌 𝑎 𝑏𝑋 𝑒 where a is the intercept b.

Librarydrc libraryggplot2 MMmodel. Now we are ready to estimate these two unknown parameters in the model using the method of least squares. LinearRegressionModel model lrfit vectorData.

I then fit this into a linear regression model. To identify the best combination of parameter values for the model I used GridSearchCV. We constructed box plots and made confidence intervals for the mean for both within-subjects MAE and within-subjects MSE.

This formula describes best possible linear model for dependence between price and phone parameters. VectorAssembler assembler new VectorAssembler setInputCols new String minute value setOutputCol features. In other words it represents the strength of the fit however it does not say anything about the model itself it.

We also investigated why the linear mixed model didnt do much better than the fixed effects only linear. To perform a simple linear regression analysis and check the results you need to run two lines of code. The mean value of the response variable when x 0.

Linear Regression Model Consider the linear regression model where Xi 1 X2i Xki is a k x 1 vector of explanatory variables 3 1 3k is a k x 1 vector of coefficients and ui is a random error term. Financial Econometrics Univariate Time Series. Y µ α β γ ε.

While the model must be linear in the parameters you can raise an independent variable by an exponent to fit a curve. Training linear models like the ones described above are typically done by minimizing the least squares criterion. The mean squared error of prediction is M SE Y cd EY Y cd2 M S E Y c d E Y Y c d 2 In this section we will identify the linear predictor that minimizes the mean squared error.

Lbeta sum_i1N y_i - beta_0 - beta_1 x_i1 - beta_2 x_i2 - 2 This is why the method is called least squares - we are minimizing the squared prediction errors. This often works extremely well but in cases where we have. We have obtained the hypothesized form in Section 21 and we have collected sample data in Section 22.

How To Choose Between Linear And Nonlinear Regression Statistics By Jim

Linear Regression Explained A High Level Overview Of Linear By Jason Wong Towards Data Science

How To Interpret Regression Models That Have Significant Variables But A Low R Squared Statistics By Jim